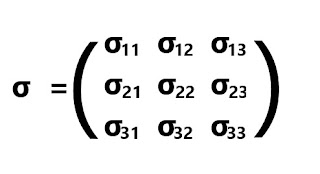Tensor Analysis
[ 1 ] Introduction :
- Tensor Are Generalization Of Scalars And Vectors.
- Tensor Are Important In Many Areas Of Physics Including
General Relativity And Electrodynemics.
- A Quantity That Did Not Change Under Rotation Of A Coordinate
System Was Labeled As A Scalar.
- A Scalar Is Specified By One Real Number And Is A Tensor Of
Rank Zero.
- A Quantity Where Components Change Under Rotation Of A
Coordinate System Was Called Vector.
- Tensor Of Order Zero Are Just Scalars .
- Tensor Of Order One Are Just Vectors.
- Tensor Of Order Two Has 3^2 = 9 Components.
- In General A Tensor Of Order N Has 3^N Components.
- Second Order Tensor Are Most Useful In Application.
- Lets Us Write Ohm's Law In The Usual From
Example :
J = σE
Where
J Is Current Density
σ Is Conductivity
E Is Electric Field
- If We Have Isotropic Medium The Conductivity Is A Scalar And
For The Anisotropic Medium Current Density In The X Direction
May So X
Component Of Current Density May Define As
J1 = σ11E1 + σ12E2
+ σ13E3
- In General Ji = ∑ σinEn
- So Ordinary In The Dimension Space The Scaler Conductivity Σ
Has Given Set Of Nine Elments.
- This Array Of Nine Elements Actual Form Tensor.
[ 2 ] Types Of Tensor :
- There Are Three Types Of Tensor
(1) Covariant Tensors
(2) Contravariant Tensor
(3) Mixed Tensor
(1) Covariant Tensors :
(2) Contravariant Tensor :

(3) Mixed Tensor :

[ 3 ] Tensors Applications :
(1) Classical Mechanics:
- Tensors Are Used To Describe Physical Quantities Such As
Force, Velocity, And Momentum In
Three-Dimensional Space.
- They Are Used In Stress Analysis To Study Deformation,
Elasticity, And Fluid Flow.
(2) Quantum Mechanics:
- Tensors Represent Operators And State Vectors In Quantum
Mechanics, Enabling Calculations Of Particle Behavior And
Properties.
(3) Relativity:
- Tensors Are Fundamental In The Formulation Of Einstein's
General Theory Of Relativity, Describing The Curvature Of
Spacetime And The Behavior Of Gravitation.
(4) Fluid Dynamics:
- Tensors Are Employed To Describe Stress, Strain, And Velocity
Fields In Fluid Flow
Simulations And Analyses.
(5) Electromagnetism:
- Tensors Describe The Electromagnetic Field And Its
Interactions, Enabling Predictions Of Electric And Magnetic
Phenomena.
(6) Material Science:
- Tensors Help Describe The Mechanical, Thermal, And
Electrical Properties Of Materials In Various Configurations
And Under Different Conditions.
(7) Computer Graphics And Computer Vision:
- Tensors Are Used In Image And Video Processing, Pattern
Recognition, And Rendering Techniques.
(8) Machine Learning And Deep Learning:
- Tensors Are Foundational For Representing Data In Neural
Networks And For Performing Operations In Training And
Inference.
(9) Medical Imaging:
- Tensors Are Used In Medical Imaging Techniques Like
Diffusion Tensor Imaging (DTI) To Analyze And Visualize
Tissue Structures.
(10) Geophysics And Seismology:
- Tensors Are Used To Model And Analyze Seismic Data And
Study The Behavior Of The Earth's Crust.
(11) Geometry And Topology:
- Tensors Play A Role In Describing Curvature, Torsion, And\
Other Geometric Properties Of
Surfaces And Spaces.
(12) Economics And Social Sciences:
- Tensors Have Been Applied To Analyze Multivariate Data
And Relationships In Economic And Social Systems.
(13) Environmental Science:
- Tensors Can Be Used To Analyze Complex Environmental
Data Sets, Such As Those Involving Multiple Variables And
Locations.
(14) Control Systems:
- Tensors Are Used In Control Theory To Model And Analyze
Dynamic Systems And Their Behavior.
(15) Astronomy And Astrophysics:
- Tensors Help Describe Celestial Objects, Their Motions, And
Interactions.
#TensorAnalysis
#TensorCalculus
#MultilinearAlgebra
#CovariantDerivative
#TensorFields
#RiemannianGeometry
#DifferentialGeometry
#CurvatureTensors
#ChristoffelSymbols
#SymmetricTensors
#ContravariantTensors
#CovariantTensors
#TensorProducts
#EinsteinNotation
#GeometricAlgebra
#ManifoldTheory
#GeneralRelativity
#FluidDynamics
#ContinuumMechanics
#ElectromagneticTensors